C#, C++ and Java Containers

C#/NET C++/STL Java

C#/.NET Fundamentals: Choosing the Right Collection Class

The .NET Base Class Library (BCL) has a wide array of collection classes at your disposal which make it easy to manage collections of objects. While it's great to have so many classes available, it can be daunting to choose the right collection to use for any given situation. As hard as it may be, choosing the right collection can be absolutely key to the performance and maintainability of your application!

This post will look at breaking down any confusion between each collection and the situations in which they excel. We will be spending most of our time looking at the System.Collections.Generic namespace, which is the recommended set of collections.

The Generic Collections: System.Collections.Generic namespace

The generic collections were introduced in .NET 2.0 in the System.Collections.Generic namespace. This is the main body of collections you should tend to focus on first, as they will tend to suit 99% of your needs right up front.

It is important to note that the generic collections are unsynchronized. This decision was made for performance reasons because depending on how you are using the collections its completely possible that synchronization may not be required or may be needed on a higher level than simple method-level synchronization. Furthermore, concurrent read access (all writes done at beginning and never again) is always safe, but for concurrent mixed access you should either synchronize the collection or use one of the concurrent collections.

So let's look at each of the collections in turn and its various pros and cons, at the end we'll summarize with a table to help make it easier to compare and contrast the different collections.

The Associative Collection Classes

Associative collections store a value in the collection by providing a key that is used to add/remove/lookup the item. Hence, the container associates the value with the key. These collections are most useful when you need to lookup/manipulate a collection using a key value. For example, if you wanted to look up an order in a collection of orders by an order id, you might have an associative collection where they key is the order id and the value is the order.

The Dictionary<TKey,TVale> is probably the most used associative container class. The Dictionary<TKey,TValue> is the fastest class for associative lookups/inserts/deletes because it uses a hash table under the covers. Because the keys are hashed, the key type should correctly implement GetHashCode() and Equals() appropriately or you should provide an external IEqualityComparer to the dictionary on construction. The insert/delete/lookup time of items in the dictionary is amortized constant time - O(1) - which means no matter how big the dictionary gets, the time it takes to find something remains relatively constant. This is highly desirable for high-speed lookups. The only downside is that the dictionary, by nature of using a hash table, is unordered, so you cannot easily traverse the items in a Dictionary in order.

The SortedDictionary<TKey,TValue> is similar to the Dictionary<TKey,TValue> in usage but very different in implementation. The SortedDictionary<TKey,TValye> uses a binary tree under the covers to maintain the items in order by the key. As a consequence of sorting, the type used for the key must correctly implement IComparable<TKey> so that the keys can be correctly sorted. The sorted dictionary trades a little bit of lookup time for the ability to maintain the items in order, thus insert/delete/lookup times in a sorted dictionary are logarithmic - O(log n). Generally speaking, with logarithmic time, you can double the size of the collection and it only has to perform one extra comparison to find the item. Use the SortedDictionary<TKey,TValue> when you want fast lookups but also want to be able to maintain the collection in order by the key.

The SortedList<TKey,TValue> is the other sorted associative container class in the generic containers. Once again SortedList<TKey,TValue>, like SortedDictionary<TKey,TValue>, uses a key to sort key-value pairs. Unlike SortedDictionary, however, items in a SortedList are stored as sorted array of items. This means that insertions and deletions are linear - O(n) - because deleting or adding an item may involve shifting all items up or down in the list. Lookup time, however is O(log n) because the SortedList can use a binary search to find any item in the list by its key. So why would you ever want to do this? Well, the answer is that if you are going to load the SortedList up-front, the insertions will be slower, but because array indexing is faster than following object links, lookups are marginally faster than a SortedDictionary. Once again I'd use this in situations where you want fast lookups and want to maintain the collection in order by the key, and where insertions and deletions are rare.

The Non-Associative Containers

The other container classes are non-associative. They don't use keys to manipulate the collection but rely on the object itself being stored or some other means (such as index) to manipulate the collection.

The List<T> is a basic contiguous storage container. Some people may call this a vector or dynamic array. Essentially it is an array of items that grow once its current capacity is exceeded. Because the items are stored contiguously as an array, you can access items in the List<T> by index very quickly. However inserting and removing in the beginning or middle of the List<T> are very costly because you must shift all the items up or down as you delete or insert respectively. However, adding and removing at the end of a List<T> is an amortized constant operation - O(1). Typically List<T> is the standard go-to collection when you don't have any other constraints, and typically we favor a List<T> even over arrays unless we are sure the size will remain absolutely fixed.

The LinkedList<T> is a basic implementation of a doubly-linked list. This means that you can add or remove items in the middle of a linked list very quickly (because there's no items to move up or down in contiguous memory), but you also lose the ability to index items by position quickly. Most of the time we tend to favor List<T> over LinkedList<T> unless you are doing a lot of adding and removing from the collection, in which case a LinkedList<T> may make more sense.

The HashSet<T> is an unordered collection of unique items. This means that the collection cannot have duplicates and no order is maintained. Logically, this is very similar to having a Dictionary<TKey,TValue> where the TKey and TValue both refer to the same object. This collection is very useful for maintaining a collection of items you wish to check membership against. For example, if you receive an order for a given vendor code, you may want to check to make sure the vendor code belongs to the set of vendor codes you handle. In these cases a HashSet<T> is useful for super-quick lookups where order is not important. Once again, like in Dictionary, the type T should have a valid implementation of GetHashCode() and Equals(), or you should provide an appropriate IEqualityComparer<T> to the HashSet<T> on construction.

The SortedSet<T> is to HashSet<T> what the SortedDictionary<TKey,TValue> is to Dictionary<TKey,TValue>. That is, the SortedSet<T> is a binary tree where the key and value are the same object. This once again means that adding/removing/lookups are logarithmic - O(log n) - but you gain the ability to iterate over the items in order. For this collection to be effective, type T must implement IComparable<T> or you need to supply an external IComparer<T>.

Finally, the Stack<T> and Queue<T> are two very specific collections that allow you to handle a sequential collection of objects in very specific ways. The Stack<T> is a last-in-first-out (LIFO) container where items are added and removed from the top of the stack. Typically this is useful in situations where you want to stack actions and then be able to undo those actions in reverse order as needed. The Queue<T> on the other hand is a first-in-first-out container which adds items at the end of the queue and removes items from the front. This is useful for situations where you need to process items in the order in which they came, such as a print spooler or waiting lines.

So that's the basic collections. Let's summarize what we've learned in a quick reference table.

The Original Collections: System.Collections namespace

The original collection classes are largely considered deprecated by developers and by Microsoft itself. In fact they indicate that for the most part you should always favor the generic or concurrent collections, and only use the original collections when you are dealing with legacy .NET code.

Because these collections are out of vogue, let's just briefly mention the original collection and their generic equivalents:

• ArrayList
  • A dynamic, contiguous collection of objects.
  • Favor the generic collection List<T> instead.
• Hashtable
  • Associative, unordered collection of key-value pairs of objects.
  • Favor the generic collection Dictionary<TKey,TValue> instead.
• Queue
  • First-in-first-out (FIFO) collection of objects.
  • Favor the generic collection Queue<T> instead.
• SortedList
  • Associative, ordered collection of key-value pairs of objects.
  • Favor the generic collection SortedList<T> instead.
• Stack
  • Last-in-first-out (LIFO) collection of objects.
  • Favor the generic collection Stack<T> instead.

In general, the older collections are non-type-safe and in some cases less performant than their generic counterparts. Once again, the only reason you should fall back on these older collections is for backward compatibility with legacy code and libraries only.

The Concurrent Collections: System.Collections.Concurrent namespace

The concurrent collections are new as of .NET 4.0 and are included in the System.Collections.Concurrent namespace. These collections are optimized for use in situations where multi-threaded read and write access of a collection is desired.

The concurrent queue, stack, and dictionary work much as you'd expect. The bag and blocking collection are more unique. Below is the summary of each with a link to a blog post I did on each of them.

• ConcurrentQueue
  • Thread-safe version of a queue (FIFO).
• ConcurrentStack
  • Thread-safe version of a stack (LIFO).
• ConcurrentBag
  • Thread-safe unordered collection of objects.
  • Optimized for situations where a thread may be bother reader and writer.
• ConcurrentDictionary
  • Thread-safe version of a dictionary.
  • Optimized for multiple readers (allows multiple readers under same lock).
• BlockingCollection
  • Wrapper collection that implement producers & consumers paradigm.
  • Readers can block until items are available to read.
  • Writers can block until space is available to write (if bounded).

Summary

The .NET BCL has lots of collections built in to help you store and manipulate collections of data. Understanding how these collections work and knowing in which situations each container is best is one of the key skills necessary to build more performant code. Choosing the wrong collection for the job can make your code much slower or even harder to maintain if you choose one that doesn't perform as well or otherwise doesn't exactly fit the situation.

Remember to avoid the original collections and stick with the generic collections.  If you need concurrent access, you can use the generic collections if the data is read-only, or consider the concurrent collections for mixed-access if you are running on .NET 4.0 or higher.

.Net Version when Collections are Available

[ Top ]

C++ STL Container Templates

• C = amortized constant time
• Overhead indicates approximate per-element additional heap space required in bytes. Based on the version of the STL that shipped with Visual Studio 6.0.
• Inserting at the end of a vector may cause the vector to be resized; resizing a vector is O(N). However, the amortized time complexity for vector insertions at the end is constant.
• slist included for comparison only. Singly-linked lists are not standard STL containers.

[ Top ]

Java Performance

Java JDK 1.6 Util package

• See JavaTree for tool to generate java class diagrams
• See Android/classtree for Android Java class diagrams

Java Container Templates

http://docs.oracle.com/javase/tutorial/collections/implementations/

		Implementations
		Hash Table	Resizable Array	Balanced Tree	Linked List	Hash Table + Linked List
Interfaces	Set	HashSet		TreeSet		LinkedHashSet
	List		ArrayList		LinkedList
	Deque		ArrayDeque		LinkedList
	Map	HashMap		TreeMap		LinkedHashMap

---

http://docs.oracle.com/javase/tutorial/collections/interfaces/index.html

http://docs.oracle.com/javase/6/docs/api/java/util/package-summary.html

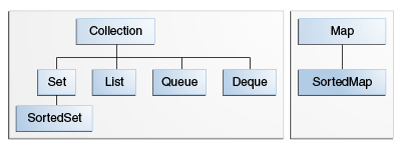
The core collection interfaces encapsulate different types of collections, which are shown in the figure below. These interfaces allow collections to be manipulated independently of the details of their representation. Core collection interfaces are the foundation of the Java Collections Framework. As you can see in

Note that all the core collection interfaces are generic. For example, this is the declaration of the Collection interface.

public interface Collection<E>...

The <E> syntax tells you that the interface is generic. When you declare a Collection instance you can and should specify the type of object contained in the collection. Specifying the type allows the compiler to verify (at compile-time) that the type of object you put into the collection is correct, thus reducing errors at runtime. For information on generic types, see the

When you understand how to use these interfaces, you will know most of what there is to know about the Java Collections Framework. This chapter discusses general guidelines for effective use of the interfaces, including when to use which interface. You'll also learn programming idioms for each interface to help you get the most out of it.

To keep the number of core collection interfaces manageable, the Java platform doesn't provide separate interfaces for each variant of each collection type. (Such variants might include immutable, fixed-size, and append-only.) Instead, the modification operations in each interface are designated optional - a given implementation may elect not to support all operations. If an unsupported operation is invoked, a collection throws an UnsupportedOperationException. Implementations are responsible for documenting which of the optional operations they support. All of the Java platform's general-purpose implementations support all of the optional operations.

The following list describes the core collection interfaces:

• Collection - the root of the collection hierarchy. A collection represents a group of objects known as its elements. The Collection interface is the least common denominator that all collections implement and is used to pass collections around and to manipulate them when maximum generality is desired. Some types of collections allow duplicate elements, and others do not. Some are ordered and others are unordered. The Java platform doesn't provide any direct implementations of this interface but provides implementations of more specific subinterfaces, such as Set and List. Also see The Collection Interface section.
• Set - a collection that cannot contain duplicate elements. This interface models the mathematical set abstraction and is used to represent sets, such as the cards comprising a poker hand, the courses making up a student's schedule, or the processes running on a machine. See also The Set Interface section.
• List - an ordered collection (sometimes called a sequence). Lists can contain duplicate elements. The user of a List generally has precise control over where in the list each element is inserted and can access elements by their integer index (position). If you've used Vector, you're familiar with the general flavor of List. Also see The List Interface section.
• Queue - a collection used to hold multiple elements prior to processing. Besides basic Collection operations, a Queue provides additional insertion, extraction, and inspection operations.

  Queues typically, but do not necessarily, order elements in a FIFO (first-in, first-out) manner. Among the exceptions are priority queues, which order elements according to a supplied comparator or the elements' natural ordering. Whatever the ordering used, the head of the queue is the element that would be removed by a call to remove or poll. In a FIFO queue, all new elements are inserted at the tail of the queue. Other kinds of queues may use different placement rules. Every Queue implementation must specify its ordering properties. Also see The Queue Interface section.

• Deque - a collection used to hold multiple elements prior to processing. Besides basic Collection operations, a Deque provides additional insertion, extraction, and inspection operations.

  Deques can be used both as FIFO (first-in, first-out) and LIFO (last-in, first-out). In a deque all new elements can be inserted, retrieved and removed at both ends. Also see The Deque Interface section.

• Map - an object that maps keys to values. A Map cannot contain duplicate keys; each key can map to at most one value. If you've used Hashtable, you're already familiar with the basics of Map. Also see The Map Interface section.

The last two core collection interfaces are merely sorted versions of Set and Map:

• SortedSet - a Set that maintains its elements in ascending order. Several additional operations are provided to take advantage of the ordering. Sorted sets are used for naturally ordered sets, such as word lists and membership rolls.
• SortedMap - a Map that maintains its mappings in ascending key order. This is the Map analog of SortedSet. Sorted maps are used for naturally ordered collections of key/value pairs, such as dictionaries and telephone directories.

---

Java-Latte Learn with a sip of Latte, September 24, 2013 by pardeep k

http://java-latte.blogspot.com/2013/09/java-collection-arraylistvectorlinkedli.html

Key Interfaces and Classesof Collection Framework

Collection	Set	SortedSet
List	Map	SortedMap
Queue	NavigableSet	NavigableMap

Key Classes of the Collections Framework

Maps	Sets	Lists	Queues	Utilities
HashMap	HashSet	ArrayList	PriorityQueue	Collections
HashTable	LinkedHashSet	Vector		Arrays
TreeMap	TreeSet	LinkedList
LinkedHashMap

---

"Concise presentations of java programming practices, tasks, and conventions, amply illustrated with syntax highlighted code examples." http://www.javapractices.com/topic/TopicAction.do?Id=65

Here's a guide for selecting the proper implementation of a Set, List, or Map. It was compiled for Java 1.4. Many additions have been made to the Collections Framework since then (notably the Queue and Deque interfaces, and various items in java.util.concurrent). These later additions have been omitted here, since this briefer summary should suffice for most cases.

The best general purpose or 'primary' implementations are likely ArrayList, LinkedHashMap, and LinkedHashSet. Their overall performance is better, and you should use them unless you need a special feature provided by another implementation. That special feature is usually ordering or sorting.

For convenience, "ordering" will here refer to the order of items returned by an Iterator, and "sorting" will here refer to sorting items according to Comparable or Comparator.
 

Interface	HasDuplicates?	Implementations					Historical
Set	no	HashSet	...	LinkedHashSet	...	TreeSet	...
List	yes	...	ArrayList	...	LinkedList	...	Vector, Stack
Map	no duplicate keys	HashMap	...	LinkedHashMap	...	TreeMap	Hashtable, Properties

Principal features of non-primary implementations:

• HashMap has slightly better performance than LinkedHashMap, but its iteration order is undefined
• HashSet has slightly better performance than LinkedHashSet, but its iteration order is undefined
• TreeSet is ordered and sorted, but slower
• TreeMap is ordered and sorted, but slower
• LinkedList has fast adding to the start of the list, and fast deletion from the interior via iteration

Iteration order for above implementations:

• HashSet - undefined
• HashMap - undefined
• LinkedHashSet - insertion order
• LinkedHashMap - insertion order of keys (by default), or 'access order'
• ArrayList - insertion order
• LinkedList - insertion order
• TreeSet - ascending order, according to Comparable / Comparator
• TreeMap - ascending order of keys, according to Comparable / Comparator

For LinkedHashSet and LinkedHashMap, the re-insertion of an item does not affect insertion order.

For LinkedHashMap, 'access order' is from the least recent access to the most recent access. In this context, only calls to get, put, and putAll constitute an access, and only calls to these methods affect access order.

While being used in a Map or Set, these items must not change state (hence, it's recommended that these items be immutable objects):

• keys of a Map
• items in a Set

Sorting requires either that:

• the stored items implement Comparable
• a Comparator for the stored objects be defined

To retain the order of a ResultSet as specified in an ORDER BY clause, insert the records into a List or a LinkedHashMap.